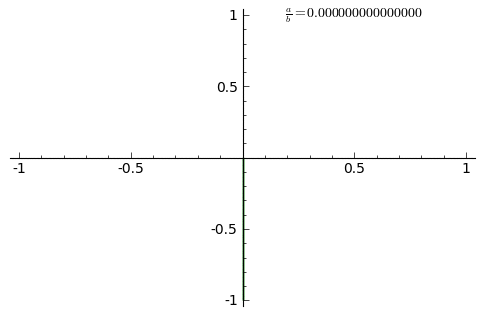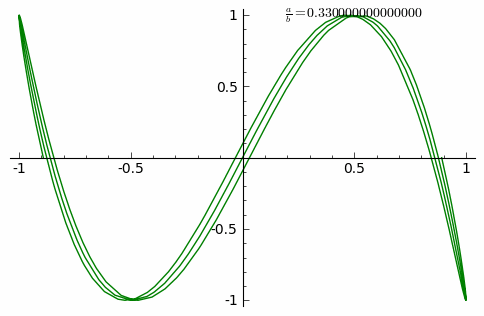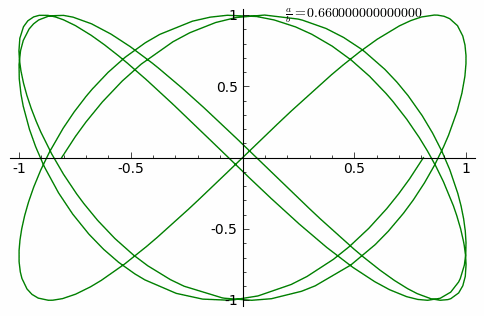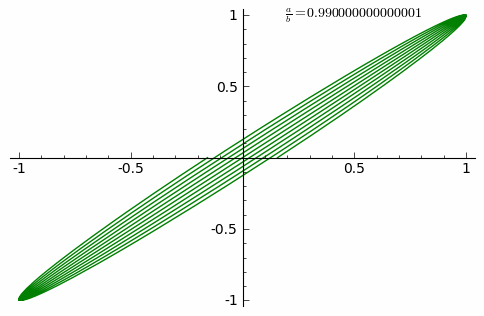Kinetic theory of gases

A Lissajous figure is a graph of the system of Parametric equation. which describe the superposition of two perpendicular oscillations in x and y directions of different angular frequency (a and b). The resulting familys of curves was investigated by Nathaniel Bowditch in 1815, and later in more detail in 1857 by Jules Antoine Lissajous (for whom it has been named). Such motions may be considered as a particular of kind of complex harmonic motion.

When Frequencies are same.

\begin{align*} \frac{x}{a}&=\sin(\omega t +\phi)~~~\frac{y}{a}=\sin\omega t\\ \frac{x}{a}&=\sin\omega t\cos\phi + \cos\omega t\sin\phi\\ \frac{x}{a}&=\frac{y}{b}\cos\phi+\sqrt{1-(\frac{y}{b})^2}\sin\phi\\ \frac{x}{a}-\frac{y}{b}\cos\phi&=\sqrt{1-\left( \frac{y}{b} \right)^2}\sin\phi\\ \frac{x^2}{a^2}+\frac{y^2}{b^2}\cos^2\phi-2\frac{xy\cos\phi}{ab}&=\sin^2\phi-\frac{y^2}{b^2}\sin^2\phi\\ \frac{x^2}{a^2}-2\frac{xy\cos\phi}{ab}+\frac{y^2}{b^2}\left(\sin^2\phi+\cos^2\phi \right)=\sin^2\phi\\ \frac{x^2}{a^2}-2\frac{xy\cos\phi}{ab}+\frac{y^2}{b^2}=\sin^2\phi\\ \frac{x^2}{a^2}+\frac{y^2}{b^2}-2\frac{xy\cos\phi}{ab}=\sin^2\phi\\ \end{align*} $$\frac{x}{a}=\sin(\omega t+\phi)~~~~~~~~~~\frac{y}{b}=\sin(\omega t)$$

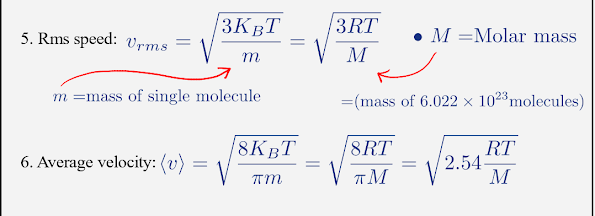
$$\langle v \rangle=\sqrt{\frac{8K_BT}{\pi m}}=\sqrt{\frac{8RT}{\pi M}}=\sqrt{2.54\frac{RT}{M}}$$